Konsep Irisan Kerucut Parabola

 | 
Konsep Irisan Kerucut Parabola - Suatu Kerucut jika dipotong oleh sebuah bidang datar maka akan menghasilkan beberapa kemungkinan bentuk yaitu lingkaran, parabola, elips, dan hipebola. Bentuk-bentuk ini banyak aplikasinya, misalnya fokus dari suatu hiperbola digunakan dalamlong distance radio navigation system, sifat-sifat elips diaplikasikan pada lithotripter (alat penghancur batu ginjal).
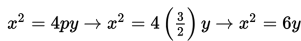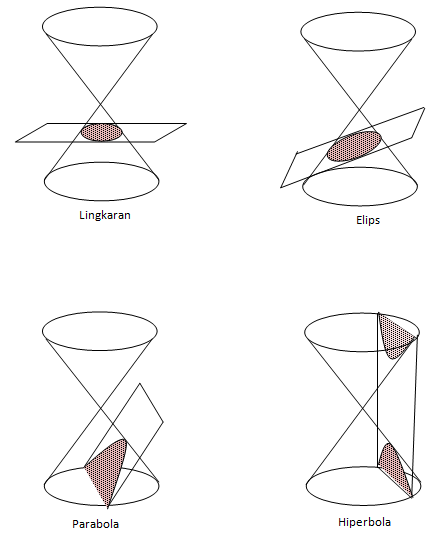
Parabola
Parabola didefinisikan sebagai kumpulan titik-titik P pada suatu bidang datar yang berjarak sama dari sebuah titik F dan sebuah garis l. F adalah fokus dari parabola, dan garis l adalah direktriks dari parabola. Garis yang tegak lurus direktriks dan melalui fokus disebut sumbu simetri. Puncak (vertex) V adalah titik dimana sumbu simetri memotong parabola. Garis melalui fokus sejajar direktriks dan ujung-ujungnya pada parabola, yaitu AB disebut Latus rectum.
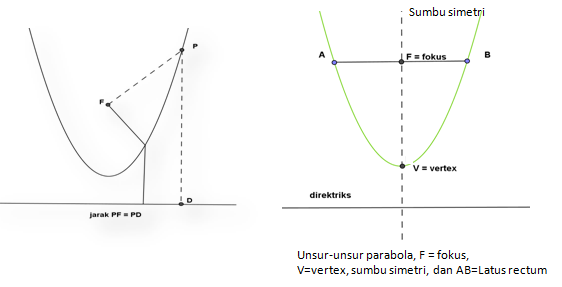
Mari kita perhatikan grafik parabola berikut ini!
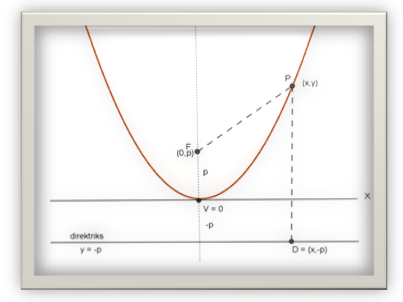
Jarak titik P (x,y) dengan F (0,p) sama dengan jarak P (x,y) dengan D (x,-p) sehingga jarak PF = Jarak PD.
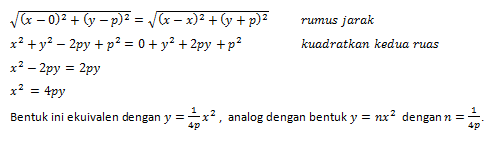
Persamaan x2 = 4py adalah bentuk sederhana dari persamaan parabola dengan
• titik puncak V (0,0)
• terbuka keatas
• sumbu Y sebagai sumbu simetri
• titik fokus terletak pada sumbu Y dengan koordinat (0,p)
• persamaan direktriks y = -p.
Selain garis arah atau direktriks yang mendatar , kita juga mengenal garis direktriks yang tegak lurus dengan persamaan parabolanya.

Persamaan Parabola dengan puncak (a , b) dan sumbu simetri sejajar sumbu Y adalah :
(x – a)2 = 4p(y-b)
  1. Koordinat puncak V (a , b)
  2. p negatif parabola terbuka ke bawah, p positif parabola terbuka ke atas
  3. Koordinat fokus F (a, b+p)
  4. Persamaan direktriks y = b - p
  5. Panjang latus rectum = 4|p|

Persamaan Parabola dengan puncak (a,b), sumbu simetri sejajar sumbu X adalah : 
(y – b)2 = 4p(x – a)
  1. Koordinat puncak V(a,b)
  2. p negatif parabola terbuka ke kiri, p positif parabola terbuka ke kanan, p≠0
  3. Koordinat fokus F(a+p,b)
  4. Persamaan direktriks X = a-p
  5. Panjang latus rectum = 4|p|

Untuk meningkatkan pemahaman kalian, mari kita cermati beberapa soal berikut ini.

Contoh 1 : Grafik parabola (y-2)2 = 16(x-2) terbuka kemana?

Pembahasan :
Persamaan parabola (y-2)2 = 16(x-2) artinya 4p = 16 sehingga nilai p adalah 4. nilai p positif maka parabola terbuka ke kanan.

Contoh 2 : Tentukan persamaan parabola dengan puncak (0,0) dan fokus (0,3/2)

Pembahasan :
Persamaan parabola dengan puncak (0,0) ada dua yaitu y2 = 4px atau x2 = 4py.
Karena titik fokus (0,3/2) terletak pada sumbu Y, maka sumbu simetrinya adalah sumbu Y.
Dengan demikian, persamaan parabola yang dimaksud adalah : x2 = 4py
Titik fokus (0 , 3/2) = (0 , p) <=> p= 3/2
Share: