Luas Daerah antara Kurva dan Sumbu Y

Luas Daerah antara Kurva dan Sumbu Y - Pada topik sebelumnya, kalian telah belajar tentang luas daerah yang dibatasi oleh kurva dan sumbu-x. Setelah mempelajari topik tersebut, kalian tentu telah menguasai persoalan-persoalan yang berhubungan dengan luas daerah yang dibatasi oleh kurva dan sumbu-x bukan? Namun, tahukah kalian bahwa terdapat beberapa persoalan integral luas yang tidak dibatasi oleh sumbu-x? Misalnya pada gambar berikut.

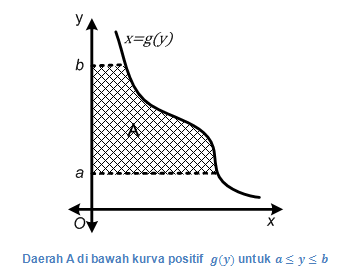
        Daerah A pada gambar di atas tidak terwakili oleh persoalan-persoalan pada luas daerah antara kurva dan sumbu-x. Untuk menghitung luas daerah A ini, kita pandang kurva sebagai fungsi dalam variabel y, yaitu x = g(y). Dengan demikian, daerah pada gambar tersebut menjadi daerah yang dibatasi oleh kurva x = g(y), y = a, y = b dan sumbu-y. Akibatnya, persoalan ini hampir serupa dengan persoalan menentukan luas daerah yang dibatasi oleh kurva dan sumbu-x, hanya saja pada kasus ini variabelnya adalah y. Bagaimana cara menentukan luas daerah antara kurva dan sumbu-y? Untuk mengetahui jawabannya, mari kita pelajari bersama-sama.

        Oleh karena persoalan luas daerah antara kurva dan sumbu-y hampir serupa dengan luas daerah antara kurva dan sumbu-x, maka persoalan-persoalan luas daerah yang dibatasi kurva dan sumbu-y juga terbagi dalam dua bahasan, yaitu kurva tidak memotong sumbu-y dan kurva memotong sumbu-y. Untuk lebih jelasnya, perhatikan uraian berikut.

🍇 Kurva Tidak Memotong Sumbu-y

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

𝓐. Daerah terletak di kanan sumbu-y

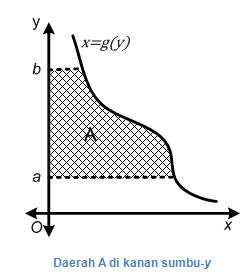
Misalkan A adalah daerah yang dibatasi kurva x = g(y), y = a, y = b, dan sumbu-y, dengan g(y) ≥ 0 (kurva di sebelah kanan dan tidak memotong sumbu-y). Luas daerah A yang dilambangkan dengan L(A) dapat kita hitung dengan integral berikut.

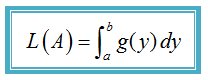
𝓑. Daerah terletak di kiri sumbu-y

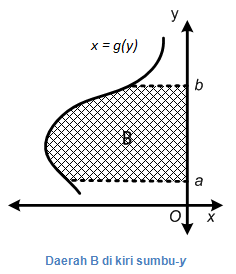
Misalkan B adalah daerah yang dibatasi kurva x = g(y), y = a, y = b, dan sumbu-y, dengan g(y) ≤ 0 (kurva di sebelah kiri dan tidak memotong sumbu-y). Pengintegralan fungsi g(y) pada interval a ≤ y ≤ b akan bernilai negatif. Oleh karena luas daerah selalu bernilai positif, maka integral luas yang dibatasi kurva g(y) ≤ 0 perlu ditambahkan dengan tanda negatif. Dengan demikian, integral luas daerah B yang dilambangkan dengan L(B) dapat kita hitung dengan integral berikut.

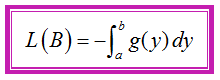
        Oleh karena terdapat dua rumus yang berbeda, maka perlu diperhatikan apakah fungsi tersebut di kanan atau di kiri sumbu-y. Untuk itu, kalian perlu mengetahui gambaran dari fungsi yang diberikan sehingga kalian dapat menentukan posisinya. Berikut adalah beberapa contoh gambar fungsi secara umum.

        Untuk memudahkan perhitungan luas daerah antara kurva dan sumbu-y, ikutilah langkah-langkah berikut ini.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

𝟙. Ubahlah fungsi y = f(x) menjadi x = g(y).

𝟚. Hitunglah luas daerah dengan ∫y2y1g(y)dy${\int }_{y_1}^{y_2}g(y)dy$.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Agar kalian paham cara menghitung luas daerah antara kurva--yang tidak memotong sumbu-y --dan sumbu-y, mari perhatikan contoh berikut ini.

Contoh 1

Luas daerah yang dibatasi oleh garis f(x)=2x$f(x)=2x$, y=4$y=4$, y=8$y=8$, dan sumbu-y adalah ….

Jawab:

Garis f(x)=2x$f(x)=2x$ dengan batas y=4$y=4$ dan y=8$y=8$ berada di kanan sumbu-y. Oleh karena itu, rumus yang digunakan bertanda positif.

Untuk menghitung luas daerah yang dibatasi garis tersebut, ubah dahulu fungsi dalam variabel y.

f(x)=2x⇒y=2x⇒x=y2$\begin{array}{ll}f(x)=2x& \Rightarrow y=2x\\ & \Rightarrow x=\frac{y}{2}\end{array}$

Dengan demikian, luas daerah yang dimaksud dapat dihitung dengan integral berikut.

L=∫84y2dy=y24∣∣∣84=824−424=16−4=12$\begin{array}{rl}L& ={\int }_4^8\frac{y}{2}dy\\ & ={\frac{y^2}{4}|}_4^8\\ & =\frac{8^2}{4}-\frac{4^2}{4}\\ & =16-4\\ & =12\end{array}$

Jadi, luas daerah yang dibatasi oleh garis f(x)=2x$f(x)=2x$, y=4$y=4$, y=8$y=8$, dan sumbu-y adalah 12 satuan luas.

Contoh 2

Luas daerah yang dibatasi oleh garis g(y)=y−3‾‾‾‾‾√−2$g(y)=\sqrt{y-3}-2$, y=3$y=3$, y=6$y=6$, dan sumbu-yadalah ….

Jawab:

Garis g(y)=y−3‾‾‾‾‾√−2$g(y)=\sqrt{y-3}-2$ dengan batas y=3$y=3$ dan y=6$y=6$ berada di kiri sumbu-y. Oleh karena itu, rumus yang digunakan bertanda negatif.

Perhatikan bahwa semua fungsi dan batas integrasi sudah dalam variabel y. Dengan demikian, luas daerah yang dibatasi garis tersebut adalah:

L=−∫63y−3‾‾‾‾‾√−2dy$L=-{\int }_3^6\sqrt{y-3}-2dy$

Misalkan u=y−3$u=y-3$, maka du=dy$du=dy$

Untuk y=3$y=3$ ⇒ u=0$u=0$

Untuk y=6$y=6$ ⇒ u=3$u=3$

Dengan demikian, diperoleh:

L=−∫63y−3‾‾‾‾‾√−2dy=−∫30u‾√−2du=−(u32(32)−2u)∣∣∣30=−((23332−2⋅3)−0)=6−23‾√$\begin{array}{ll}L& =-{\int }_3^6\sqrt{y-3}-2dy\\ & =-{\int }_0^3\sqrt{u}-2du\\ & =-{\left(\frac{u^{\frac{3}{2}}}{\left(\frac{3}{2}\right)}-2u\right)|}_0^3\\ & =-\end{array}$

$\begin{array}{l}<br>\end{array}$

$\begin{array}{l}\left(\left(\frac{2}{3}{3}^{{}^{\frac{3}{2}}}-2\cdot 3\right)-0\right)\\ & =6-2\sqrt{3}\end{array}$

Jadi, luas daerah yang dibatasi garis g(y)=y−3‾‾‾‾‾√−2$g(y)=\sqrt{y-3}-2$, y=3$y=3$, y=6$y=6$, dan sumbu-yadalah 6−23‾√$6-2\sqrt{3}$ satuan luas.

🍇 Kurva Memotong Sumbu-y

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

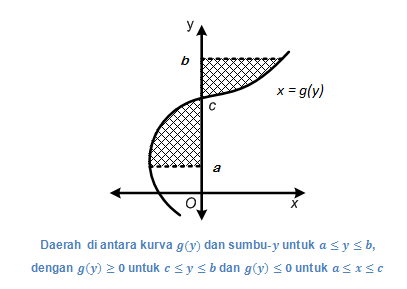
Misalkan x = g(y) adalah fungsi kontinu pada selang a ≤ y ≤ b dan g(y) memotong sumbu-y di titik y = c. g(y) ≥ 0 untuk c ≤ y ≤ b dan g(y) ≤ 0 untuk a ≤ y ≤ c. Luas daerah yang dibatasi oleh x = g(y) dan sumbu-y pada selang a ≤ y ≤ b adalah:

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

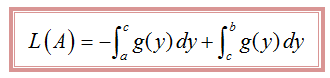
Contoh 3

Luas dari daerah yang dibatasi oleh kurva y=x3$y=x^3$, y=−4$y=-4$, y=4$y=4$, dan sumbu-y adalah ….

Jawab:

Kurva y=x3$y=x^3$ dengan batas y=−4$y=-4$ dan y=4$y=4$ memotong sumbu-y pada titik (0,0). Oleh karena itu, akan terbentuk dua daerah yaitu pada interval -4 ≤ y ≤ 0 untuk kurva negatif dan pada interval 0 ≤ y ≤ 4 untuk kurva positif.

Oleh karena integralnya dalam variabel y, maka ubah dahulu fungsi dalam variabel y.

y=x3⇒x=y√3$y=x^3\Rightarrow x=\sqrt[3]{y}$

Dengan demikian luas daerah tersebut adalah:

L=−∫0−4y√3dy+∫40y√3dy=−∫0−4y13dy+∫40y13dy=−(y43(43)∣∣∣∣0−4)+(y43(43)∣∣∣∣40)=−(0−3⋅(−4)434)+(3⋅4434−0)=3⋅413+3⋅413=64‾√3$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{ll}L& =-{\int }_{-4}^0\sqrt[3]{y}dy+{\int }_0^4\sqrt[3]{y}dy\\ & =-{\int }_{-4}^0{y}^{\frac{1}{3}}dy+{\int }_0^4{y}^{\frac{1}{3}}dy\\ & =-\left({\frac{y^{\frac{4}{3}}}{\left(\frac{4}{3}\right)}|}_{-4}^0\right)+\left({\frac{y^{\frac{4}{3}}}{\left(\frac{4}{3}\right)}|}_0^4\right)\\ & =-\end{array}$

$\begin{array}{l}\left(0-\frac{3\cdot {\left(-4\right)}^{\frac{4}{3}}}{4}\right)+\left(\frac{3\cdot 4^{\frac{4}{3}}}{4}-0\right)\\ & =3\cdot 4^{\frac{1}{3}}+3\cdot 4^{\frac{1}{3}}\\ & =6\sqrt[3]{4}\end{array}$

Jadi, luas daerah tersebut adalah 64‾√3$6\sqrt[3]{4}$ satuan luas.

Nah, kalian telah selesai belajar tentang luas daerah yang dibatasi oleh sumbu-y. Agar pemahaman kalian bertambah lagi, yuk kerjakan latihan soal-soal berikut ini.