Konsep Irisan Kerucut Hiperbola

Konsep Irisan Kerucut Hiperbola - Pada topik sebelumnya, kalian telah mempelajari konsep irisan parabola. Pada topik ini, kalian akan mempelajari konsep irisan hiperbola. Sebelum mempelajarinya, mari kita ingat kembali pengertian irisan kerucut.

1. Irisan Kerucut

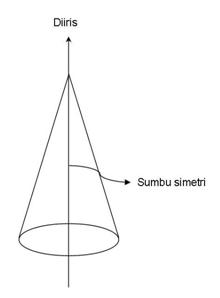
Irisan kerucut adalah tempat kedudukan titik-titik pada bidang yang perbandingan jaraknya terhadap suatu titik dan suatu garis selalu tetap.

Salah satu jenis irisan kerucut ini adalah hiperbola. Hiperbola terjadi jika kerucut diiris sejajar dengan sumbu simetri.

1. Pengertian Hiperbola Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola.

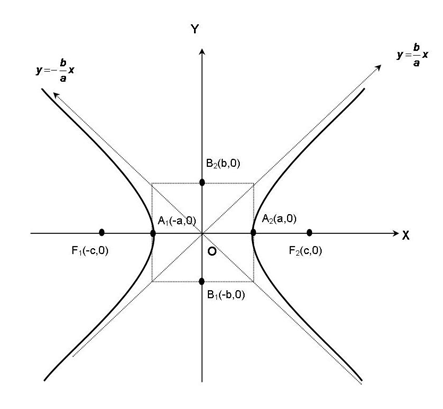
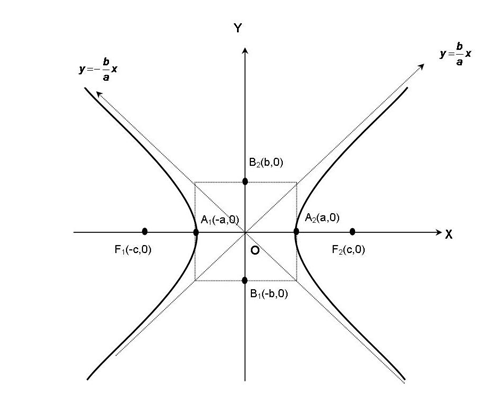
Gambar tersebut merupakan hiperbola yang berpusat di titik O(0,0).
• F1( -c, 0) dan F2(c, 0) adalah titik fokus hiperbola yang jaraknya 2c. Sementara selisih jarak yang tetap itu adalah 2a. 
• Sumbu utama adalah sumbu x, sedangkan sumbu sekawan adalah sumbu y.
• Sumbu mayor adalah A1A2, panjangnya 2a. Sumbu minor adalah B1B2, panjangnya 2b.
• Titik A1 dan A2 disebut titik puncak hiperbola yang merupakan titik potong hiperbola dengan sumbu mayor.
• Lactus rectum adalah garis vertikal yang melalui salah satu fokus, tegak lurus sumbu mayor, dan memotong hiperbola di dua titik. Panjang lactus rektum adalah

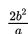
• Persamaan asimtot hiperbola adalah

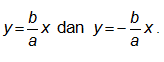
• Eksentrisitas = e = c/a , dengan e > 1.

• Persamaan garis direktriks adalah

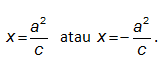
• Ketentuan khusus pada hiperbola yaitu c2 = a2 + b2.

1. Persamaan Hiperbola a. Persamaan hiperbola yang berpusat di titik (0, 0)

Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu x adalah

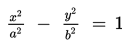
Titik fokus adalah F1(c, 0) dan F2(-c, 0).
Titik puncak adalah A1(a, 0) dan A2(-a, 0).
Persamaan asimtotnya adalah

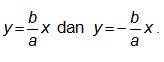
Bagaimana jika sumbu utamanya adalah sumbu y?

Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu y adalah

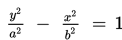
Titik fokus adalah F1(0, c) dan F2(0, -c).
Titik puncak adalah A1(0, a) dan A2(0, -a).
Persamaan asimtotnya adalah

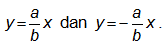
Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 1:
Tentukan persaman asimtot dari persamaan

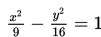
Penyelesaian:
Coba perhatikan bahwa sumbu utama persamaan hiperbola ini adalah sumbu x. Akibatnya, a2 = 9 dan b2 = 16, sehingga a = 3 dan b = 4.
Persamaan asimtotnya adalah

b. Persamaan hiperbola yang berpusat di titik (p, q)

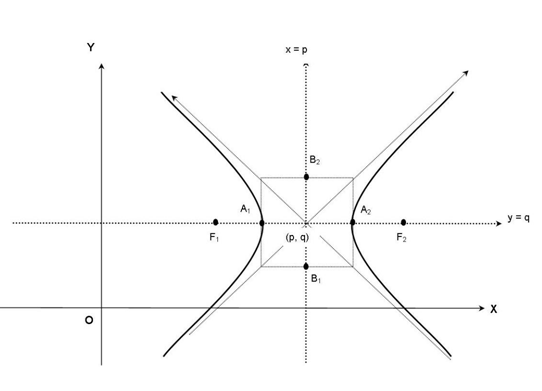
Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utamanya sejajar dengan sumbu x adalah

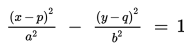
Titik fokus adalah F1(p + c, q) dan F2(p – c, q).
Titik puncak adalah A1(p + a, q) dan A2(p – a, q).
Persamaan asimtotnya adalah

Bagaimana jika sumbu utama hiperbola sejajar dengan sumbu y?
Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utama sejajar dengan sumbu y adalah

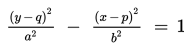
Titik fokus adalah F1(p, q + c) dan F2(p, q – c).
Titik puncak adalah A1(p, q + a) dan A2(p, q – a).
Persamaan asimtotnya adalah

Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 2:
Sebuah hiperbola mempunyai persamaan 9x2 – 4y2 – 36x – 8y + 68 = 0.
Tentukan titik pusat, titik puncak, dan titik fokus hiperbola tersebut!
Penyelesaian:
Ayo, ubah bentuk persamaan tersebut ke dalam bentuk baku.
9x2 – 4y2 – 36x – 8y + 68 = 0
9x2 – 36x – 4y2 – 8y = –68
9(x2 – 4x + 4) – 4(y2 + 2y + 1) = –68 + 36 – 4
9(x – 2)2 – 4(y + 1)2 = –36
4(y + 1)2 – 9(x – 2)2 = 36

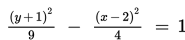
Persamaan hiperbola ini memiliki sumbu utama yang sejajar dengan sumbu y dengan a2 = 9 dan b2 = 4. Akibatnya, c2 = a2 + b2 = 9 + 4 = 13.
Titik pusat hiperbola adalah (2, -1).
Titik puncaknya adalah (2, -1 + 3) = (2, 2) dan (2, -1 – 3) = (2, -4).
Titik fokusnya adalah

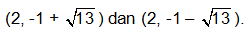
1. Persamaan Garis Singgung Hiperbola Sebuah garis digambarkan pada sebuah hiperbola. Salah satu kedudukan yang mungkin antara garis itu dan hiperbola adalah garis menyinggung hiperbola. Coba perhatikan gambar berikut.

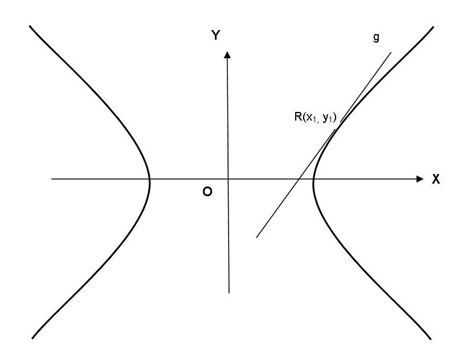
Pada gambar tersebut garis g menyinggung hiperbola pada titik R(x1, y1).
a. Persamaan garis singgung yang melalui suatu titik pada hiperbola
• Persamaan garis singgung pada suatu titik R(x1, y1) pada hiperbola

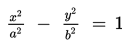
adalah

Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 3:
Coba tentukan persamaan garis singgung pada titik (9, 2) yang terletak pada hiperbola

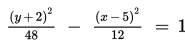
Penyelesaian:
Persamaan garis singgungnya dapat dihitung seperti berikut.

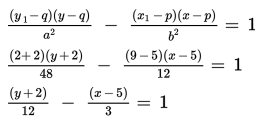
y – 4x + 10 = 0
Jadi, persamaan garis singgungnya adalah y – 4x + 10 = 0.

b. Persamaan garis singgung bergradien m pada hiperbola
Misalkan garis g yang menyinggung hiperbola tersebut bergradien m, maka:

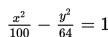
Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 4:
Tentukan persamaan garis singgung dengan gradien 1 pada hiperbola

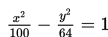
Penyelesaian:

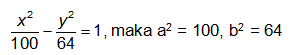
Gradien m = 1
Persamaan garis singgungnya adalah sebagai berikut.

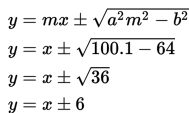
Jadi, persamaan garis singgungnya adalah y = x + 6 atau y = x – 6.