Dilatasi yang berpusat di P (0, 0) dengan Faktor Skalar k

Dilatasi yang berpusat di P (0, 0) dengan Faktor Skalar k - Sebagai warga negara Indonesia, tentunya kalian pernah melihat batik bukan?

Jika kalian amati, batik mempunyai pola atau bentuk keteraturan tertentu. Nah, bentuk keteraturan ini sebenarnya merupakan bentuk transformasi geometris.

Dilatasi merupakan salah satu transformasi geometris yang dapat kalian jumpai pada motif batik.

Apa itu dilatasi?

Yuk kita temukan jawabannya dengan mempelajari topik ini.

Definisi

Dilatasi merupakan suatu bentuk transformasi yang memindahkan suatu titik atau objek berdasarkan titik pusat dan faktor perkalian/skala tertentu.

Seperti yang telah kalian ketahui, bentuk bayangan yang dihasilkan dari translasi, refleksi, dan rotasi adalah kongruen (sama ukuran dan sebagun) dengan bangun semula. Nah, bayangan hasil dilatasi suatu bangun tidaklah kongruen dengan bangun semula. Dengan kata lain, dilatasi bukan merupakan transformasi isometri.

Tahukah kalian mengapa dilatasi bukan merupakan transformasi isometri?

Ya, sebab bayangan hasil dilatasi mengalami perubahan ukuran, yaitu diperbesar atau diperkecil, walaupun bentuk bangunnya tetap.

Konsep Dasar

Dalam topik ini kalian akan belajar mengenai dilatasi yang berpusat di titik O(0,0)$O(0,0)$dengan faktor skala k$k$.

Apa itu faktor skala?

Jika titik A′(x′,y′)$A^{\prime }(x^{\prime },y^{\prime })$ adalah hasil dilatasi dari titik A(x,y)$A(x,y)$ terhadap pusat O(0,0)$O(0,0)$ dengan faktor skala k$k$, maka faktor skala adalah perbandingan antara jarak pusat dilatasi dengan bayangan dan jarak pusat dilatasi dengan titik asal.

Dengan kata lain, k=OA′OA$k=\frac{O{A}^{{}^{\prime }}}{OA}$.

Mari kita perhatikan gambar berikut:

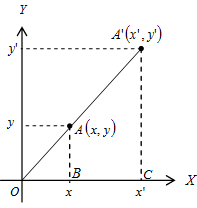
Pada gambar di atas, tampak bahwa ∆AOB$∆AOB$ dan ∆A′OC$∆A^{\prime }OC$ sebangun.

Oleh karena k=OA′OA$k=\frac{O{A}^{{}^{\prime }}}{OA}$, maka

1. OCOB=k⇔x′x=k⇔x′=kx $\frac{OC}{OB}=k\iff \frac{x^{\prime }}{x}=k\iff x^{\prime }=kx$
2. A′CAB=k⇔y′y=k⇔y′=ky $\frac{A^{\prime }C}{AB}=k\iff \frac{y^{\prime }}{y}=k\iff y^{\prime }=ky$

Dengan demikian, bayangan titik A(x,y)$A(x,y)$ oleh dilatasi [O(0,0),k]$[O(0,0),k]$ adalah A′(kx,ky)$A^{\prime }(kx,ky)$.

Lebih lanjut, notasi dari hasil dilatasi titik A(x,y)$A(x,y)$ terhadap [O(0,0),k]$[O(0,0),k]$ adalah sebagai berikut: A(x,y)−→−−[O,k]A′(kx,ky) $A(x,y)\stackrel{[O,k]}{\to }{A}^{\prime }(kx,ky)$.

Adapun persamaan matriksnya adalah (x′y′ )=(k00k )(xy ) $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$.

Contoh 1

Tentukan bayangan titik C(−6,3)$C(-6,3)$ oleh dilatasi terhadap titik O(0,0)$O(0,0)$ dengan faktor skala −12$-\frac{1}{2}$.

Penyelesaian:

Jika C′(x′,y′)$C^{\prime }(x^{\prime },y^{\prime })$ adalah koordinat titik bayangan, maka

(x′y′ )===(k00k )(xy )(−1200−12 )(−63 )(3−32 )  $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}-\frac{1}{2}& 0\\ 0& -\frac{1}{2}\end{array}\right)\left(\begin{array}{c}-6\\ 3\end{array}\right)\\ & =& \left(\begin{array}{c}3\\ -\frac{3}{2}\end{array}\right)\end{array}$

Dengan demikian, bayangan titik C(−6,3)$C(-6,3)$ oleh dilatasi terhadap titik O(0,0)$O(0,0)$ dengan faktor skala −12$-\frac{1}{2}$ adalah C′(3,−32)$C^{\prime }(3,-\frac{3}{2})$.

Contoh 2

Tentukan persamaan bayangan kurva y=x2−3x+2$y=x^2-3x+2$ oleh dilatasi dengan pusat O(0,0)$O(0,0)$ dan faktor skala 3.

Penyelesaian:

Jika titik (x′,y′)$(x^{\prime },y^{\prime })$ adalah bayangan dari titik (x,y)$(x,y)$ terhadap dilatasi yang sama dengan soal, maka

(x′y′ )===(k00k )(xy )(3003 )(xy )(3x3y )  $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}3& 0\\ 0& 3\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{c}3x\\ 3y\end{array}\right)\end{array}$

Berdasarkan uraian di atas, x=13x′$x=\frac{1}{3}{x}^{\prime }$ dan y=13y′$y=\frac{1}{3}{y}^{\prime }$.

Dengan demikian,

y=x2−3x+2 $y=x^2-3x+2$
⇔13y′=(13x′)2−3(13x′)+2 $\iff \frac{1}{3}{y}^{\prime }={\left(\frac{1}{3}{x}^{\prime }\right)}^2-3\left(\frac{1}{3}{x}^{\prime }\right)+2$
⇔13y′=19(x′)2−x′+2 $\iff \frac{1}{3}{y}^{\prime }=\frac{1}{9}{\left(x^{\prime }\right)}^2-x^{\prime }+2$
⇔y′=13(x′)2−3x′+6 $\iff y^{\prime }=\frac{1}{3}{\left(x^{\prime }\right)}^2-3x^{\prime }+6$

Jadi, persamaan bayangan kurva y=x2−3x+2$y=x^2-3x+2$ oleh dilatasi dengan pusat O(0,0)$O(0,0)$dan faktor skala 3 adalah y=13x2−3x+6