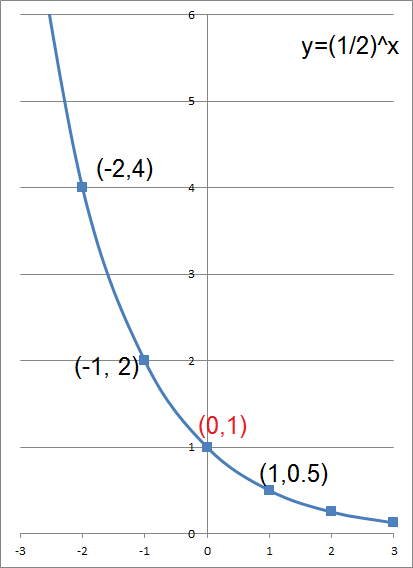
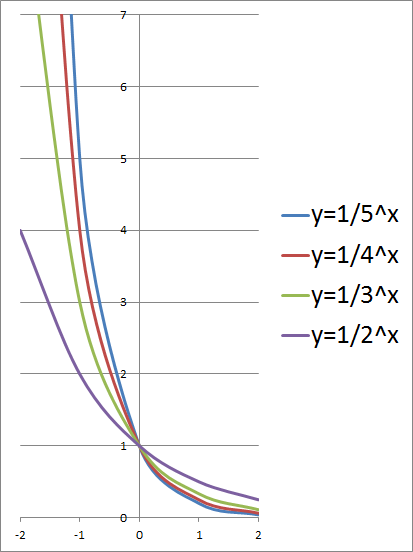
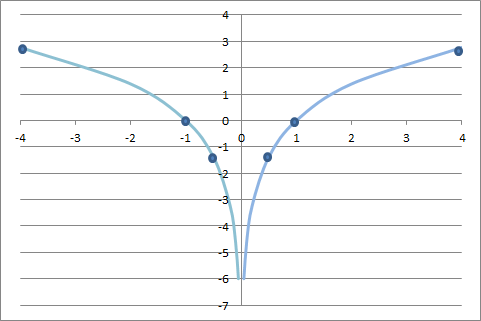
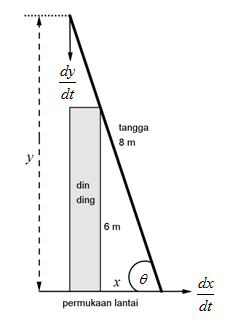
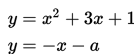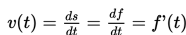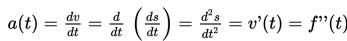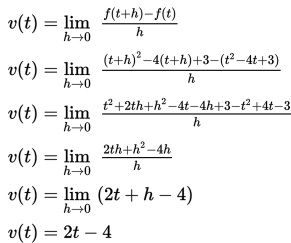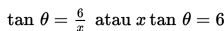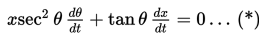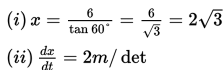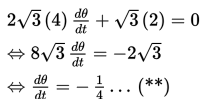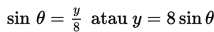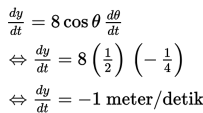Menyelesaikan sistem persamaan linear dan persamaan kuadratik secara aljabar
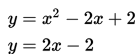
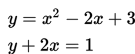
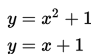
SOAL 6
Diberikan sistem persamaan linear kuadrat: y−x2=3y−x2=3 dan y−2x=2y−2x=2. Penyelesaian dari sistem persamaan linear kuadrat di atas adalah ....
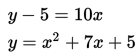
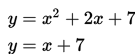
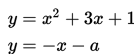
SOAL 1
Ada berapa jenis solusi yang bisa dimiliki sistem kuadrat linear?
SOAL 2
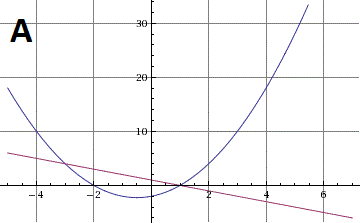
Pada titik keberapakah persamaan linear dan persamaan kuadrat berikut ini akan bersinggungan?
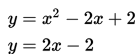
SOAL 3
Pada titik keberapakah persamaan linear dan persamaan kuadrat berikut ini akan bersinggungan?
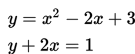
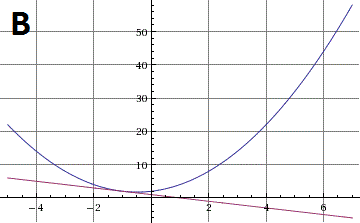
SOAL 4
Apa jawaban dari sistem persamaan linear berikut ini?
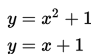
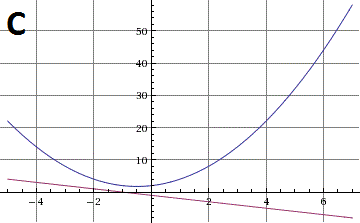
SOAL 5
Jawablah sistem persamaan linear kuadrat berikut:
Diberikan sistem persamaan linear kuadrat: y−x2=3y−x2=3 dan y−2x=2y−2x=2. Penyelesaian dari sistem persamaan linear kuadrat di atas adalah ....
SOAL 7
Manakah dari yang berikut ini yang bukan merupakan angka jawaban sistem linear kuadrat?
SOAL 8
Jawab sistem persamaan linear berikut ini:
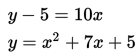
SOAL 9
Tentukan manakah dari berikut ini yang merupakan jawaban dari sistem persamaan linear berikut ini?
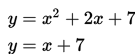
SOAL 10
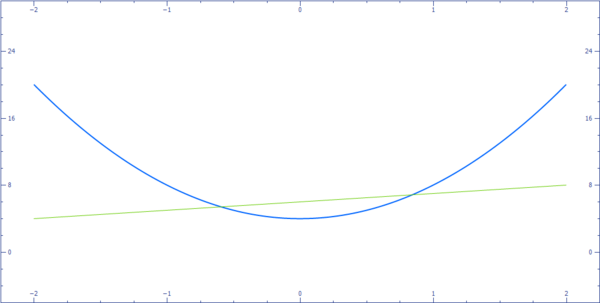
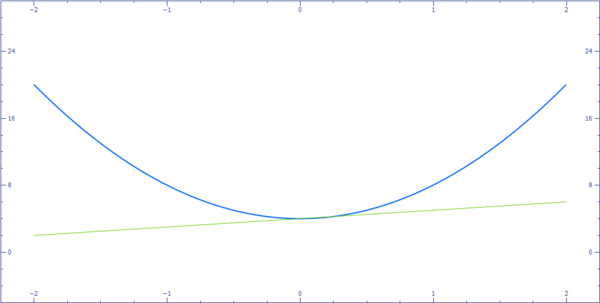
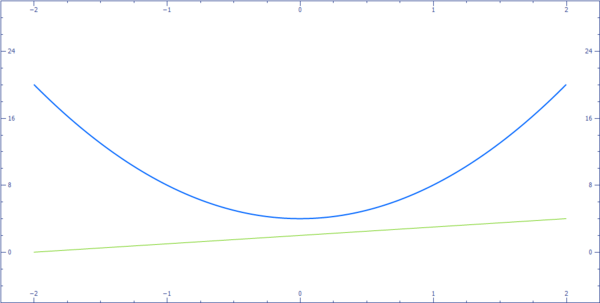
Tentukan nilai a pada sistem persamaan linear kuadrat berikut agar memiliki satu solusi riil.