Persamaan kuadrat didefinisikan sebagai suatu persamaan dengan sebuah suku atau beberapa suku berderajat derajat 2 dan tidak ada suku yang mempunyai derajat lebih dari 2. Dengan demikian, bentuknya adalah parabola.
Adapun bentuk umumnya adalah : ax2 + bx + c = 0, dimana a, b, dan c adalah suatu konstanta.
Penyelesaian dari suatu sistem persamaan kuadrat-linear merupakan titik potong antara grafik kuadrat dan grafik linear.
Dengan demikian, ada 3 kejadian yang mungkin, yaitu :
1. Dua grafik berpotongan pada 2 buah titik.
Dalam kasus ini, sistem persamaan mempunyai 2 penyelesaian real. Contoh : :
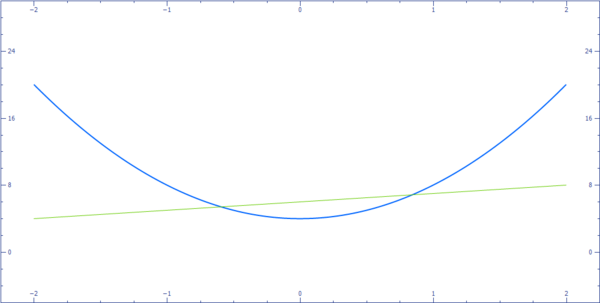
2. Grafik linear menyinggung grafik kuadrat.
Dalam kasus ini, sistem persamaan mempunyai tepat satu penyelesaian real. Berikut ini
adalah contohnya :
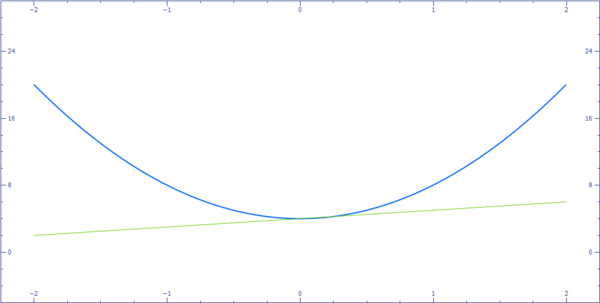
3. Dua grafik tidak berpotongan sama sekali.
Dalam kasus ini, tidak ada penyelesaian real yang diperoleh. Hal ini terjadi karena kedua grafik
tidak berpotongan. Berikut ini adalah contohnya :
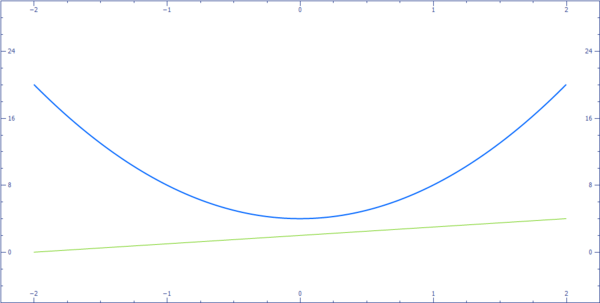
Dalam pelajaran ini, kalian akan belajar tentang bagaimana cara menyelesaikan suatu sistem persamaan yang terdiri atas persamaan linear dan persamaan kuadrat dengan menggunakan grafik. Berikut ini adalah beberapa contoh yang akan membantu kalian memahami materi ini :
Dari 3 gambar berikut ini, manakah yang merupakan sistem persamaan dengan jumlah penyelesaian real paling sedikit?
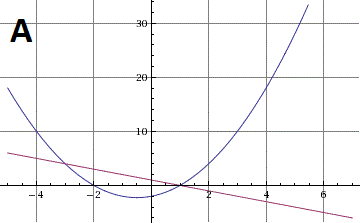
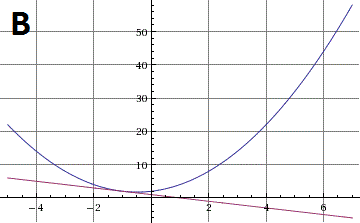
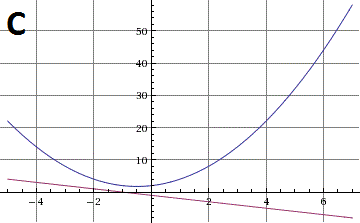
PENYELESAIAN :
Pada gambar C tidak ditemukan titik potong antara kurva dan garis. Dengan demikian, sistem pada gambar C mempunyai jumlah penyelesaian real yang paling sedikit, yaitu nol.