Komposisi Dua Translasi Berurutan

Komposisi Dua Translasi Berurutan - Salah satu jenis transformasi geometri adalah translasi.

Apakah kalian masih ingat dengan definisi dari translasi?

Ya, translasi atau pergeseran adalah jenis transformasi yang memindahkan suatu objek atau benda pada bidang datar dengan jarak dan arah tertentu.

Seperti yang kalian ketahui, panjang dan arah translasi dapat dinyatakan dalam bentuk vektor kolom.

Sebagai ilustrasi, misalkan kalian mendorong sebuah meja ke arah timur sejauh dua meter, kemudian meja tersebut kalian dorong lagi ke arah utara sejauh satu meter.

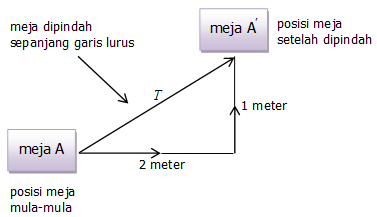
Kalian masih ingat dengan konsep vektor bukan?

Nah, vektor kolom yang mewakili pergeseran di atas adalah (21)$\left(\begin{array}{c}2\\ 1\end{array}\right)$.

Komposisi Dua Fungsi

Sewaktu kalian berada di kelas XI, kalian telah belajar mengenai komposisi dua fungsi.

Apakah kalian masih ingat dengan konsep komposisi dua fungsi?

Ya, jika nilai x$x$ dipetakan terhadap fungsi f$f$, kemudian hasil peta tersebut dipetakan terhadap fungsi g$g$, maka fungsi komposisi yang mewakili pemetaan tersebut adalah (g∘f)(x)$\left(g\circ f\right)\left(x\right)$ atau g(f(x))$g\left(f(x)\right)$.

Berdasarkan konsep tersebut, dapat kita simpulkan bahwa transformasi (T2∘T1)(x,y)=T2(T1(x,y))$\left(T_2\circ T_1\right)\left(x,y\right)=T_2\left(T_1(x,y)\right)$ menyatakan translasi titik (x,y)$(x,y)$ terhadap T1$T_1$dilanjutkan translasi terhadap T2$T_2$.

Komposisi Dua Translasi Berurutan

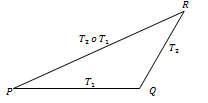
Pada gambar di atas, bayangan titik P$P$ jika ditranslasikan terhadap T2$T_2$ adalah titik Q$Q$. Adapun bayangan titik Q$Q$ terhadap translasi T1$T_1$ adalah titik R$R$.

Apa yang dapat kalian simpulkan dari gambar di atas?

Ya, bayangan titik P$P$ oleh translasi T1$T_1$ dilanjutkan oleh translasi T2$T_2$ adalah titik R$R$. Adapun dua translasi yang berurutan ini dinotasikan dengan T2∘T1$T_2\circ T_1$.

Selanjutnya, karena (PQ−→−+QR−→−=PR−→)$(\overrightarrow{PQ}+\overrightarrow{QR}=\overrightarrow{PR})$, maka dapat kita simpulkan bahwa T2∘T1=T2+T1$T_2\circ T_1=T_2+T_1$.

Nah, karena operasi penjumlahan dalam vektor kolom bersifat komutatif, maka T2∘T1=T2+T1=T1+T2=T1∘T2$T_2\circ T_1=T_2+T_1=T_1+T_2=T_1\circ T_2$

Materi di atas mudah dipahami bukan?

Yuk kita cermati dua contoh soal berikut.

Contoh 1

Diketahui titik (3,−1)$(3,-1)$ ditranslasikan terhadap T1=(11)$T_1=\left(\begin{array}{l}1\\ 1\end{array}\right)$ kemudian ditranslasikan terhadap T2=(22)$T_2=\left(\begin{array}{l}2\\ 2\end{array}\right)$.

Tentukan

• translasi tunggal yang mewakili translasi dalam soal
• bayangan titik (3,−1)$(3,-1)$

Penyelesaian:

Oleh karena T2∘T1=T2+T1=(22)+(11)=(33)$T_2\circ T_1=T_2+T_1=\left(\begin{array}{l}2\\ 2\end{array}\right)+\left(\begin{array}{l}1\\ 1\end{array}\right)=\left(\begin{array}{l}3\\ 3\end{array}\right)$, maka translasi tunggal yang mewakili translasi dalam soal adalah T=(33)$T=\left(\begin{array}{c}3\\ 3\end{array}\right)$.

Dengan demikian, T2∘T1(3−1)=(33)+(3−1)=(62)$T_2\circ T_1\left(\begin{array}{c}3\\ -1\end{array}\right)=\left(\begin{array}{c}3\\ 3\end{array}\right)+\left(\begin{array}{c}3\\ -1\end{array}\right)=\left(\begin{array}{c}6\\ 2\end{array}\right)$.

Jadi, bayangan titik (3,−1)$(3,-1)$ adalah titik (6,2)$(6,2)$.

Contoh 2

Tentukan bayangan parabola y=2x2−3x+5$y=2x^2-3x+5$ oleh translasi T2=(11)$T_2=\left(\begin{array}{c}1\\ 1\end{array}\right)$ dilanjutkan oleh translasi T1=(2−4)$T_1=\left(\begin{array}{c}2\\ -4\end{array}\right)$ .

Penyelesaian:

Oleh karena

T1∘T2===T1+T2(11 )+(2−4 )(3−3 ) $\begin{array}{lll}{T}_1\circ T_2& =& T_1+T_2\\ & =& \left(\begin{array}{c}1\\ 1\end{array}\right)+\left(\begin{array}{c}2\\ -4\end{array}\right)\\ & =& \left(\begin{array}{c}3\\ -3\end{array}\right)\end{array}$

maka

T1∘T2(xy )=(x′y′ )⇔(3−3 )+(xy )=(x′y′ )⇔(xy )=(x′−3y′+3 ) $\begin{array}{rl}& T_1\circ T_2\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)\\ & \iff \left(\begin{array}{c}3\\ -3\end{array}\right)+\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)\\ & \iff \left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{x}^{\prime }-3\\ y^{\prime }+3\end{array}\right)\end{array}$

Jika kita subtitusikan hasil di atas ke persamaan parabola y=2x2−3x+5$y=2x^2-3x+5$, maka kita peroleh hasil sebagai berikut:

y=2x2−3x+5 ⇔y′+3=2(x′−3)2−3(x′−3)+5⇔y′+3=2((x′)2−6x′+9)−3x′+9+5⇔y′+3=2(x′)2−12x′+18−3x′+14⇔y′+3=2(x′)2−15x′+32⇔y′=2(x′)2−15x′+29$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}y=2x^2-3x+5\iff y^{\prime }+3=2{\left(x^{\prime }-3\right)}^2-3\left(x^{\prime }-3\right)+5\\ \iff y^{\prime }+3=2\left({(x^{\prime })}^2-6x^{\prime }+9\right)-3x^{\prime }+9+5\end{array}$

$\begin{array}{l}\iff y^{\prime }+3=2{\left(x^{\prime }\right)}^2-12x^{\prime }+18-3x^{\prime }+14\\ \iff y^{\prime }+3=2{\left(x^{\prime }\right)}^2-15x^{\prime }+32\\ \iff y^{\prime }=2{\left(x^{\prime }\right)}^2-15x^{\prime }+29\end{array}$

Dengan demikian, bayangan parabola y=2x2−3x+5$y=2x^2-3x+5$ oleh translasi di atas adalah y=2x2−15x+29$y=2x^2-15x+29$.

Nah, kalian telah selesai mempelajari materi di atas. Ayo kerjakan latihan soal dalam topik ini.