Gusuran Searah Sumbu X

Gusuran Searah Sumbu X - 

Jika kalian baca kutipan berita di atas dengan cermat, maka kalian akan menemukan istilah 'gusur'. Sebearnya apa arti dari istilah 'gusur'? Apa hubungannya dengan matematika?

Dalam matematika, ada istilah 'gusuran' (shear). Nah, ada dua macam gusuran yang akan kalian pelajari di kelas XII ini, yaitu gusuran searah sumbu X$X$ (gusuran secara horizontal) dan gusuran searah sumbu Y$Y$ (gusuran secara vertikal).

Konsep Dasar

Dalam matematika, gusuran erat kaitannya dengan faktor skala. Jika gusuran ke arah kanan, maka faktor skala bernilai positif. Nah, jika gusuran ke arah kiri, maka faktor skala bernilai negatif.

Mari kita perhatikan ilustrasi berikut:

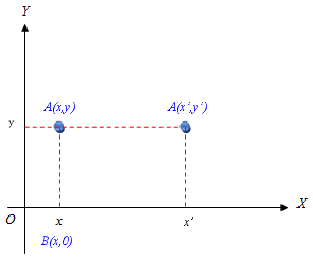
Dalam ilustrasi di atas, titik A(x,y)$A(x,y)$ digusur ke kanan hingga menjadi titik A′(x′,y′)$A^{\prime }(x^{\prime },y^{\prime })$.

Nah, yang dimaksud dengan faktor skala k$k$ adalah perbandingan jarak antara AA′$A{A}^{\prime }$ dan AB$AB$. Dengan kata lain, k=AA′AB⇔k=AA′y⇔AA′=ky$k=\frac{A{A}^{\prime }}{AB}\iff k=\frac{A{A}^{\prime }}{y}\iff A{A}^{\prime }=ky$.

Dalam ilustrasi di atas, tampak bahwa

• x′=x+AA′=x+ky$x^{\prime }=x+A{A}^{\prime }=x+ky$
• y′=y$y^{\prime }=y$

Dengan demikian, persamaan matriks yang sesuai dengan transformasi gusuran searah sumbu X$X$ dengan faktor skala k$k$ adalah (x′y′ )=(10k1 )(xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& k\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$.

Apakah kalian sudah paham dengan penjelasan di atas?

Agar kalian semakin paham, yuk kita cermati beberapa contoh soal berikut.

Contoh 1

Tentukan bayangan titik A(3,−4)$A(3,-4)$ oleh gusuran searah sumbu X$X$ dengan faktor skala k=2$k=2$.

Penyelesaian:

Oleh karena matriks transformasi dari gusuran searah sumbu X$X$ dengan faktor skala k$k$adalah (10k1 )$\left(\begin{array}{cc}1& k\\ 0& 1\end{array}\right)$, maka bayangan titik A(3,−4)$A(3,-4)$ dapat ditentukan dengan cara sebagai berikut:

(x′Ay′A )===(1021 )(xAyA )(1021 )(3−4 )(−5−4 ) $\begin{array}{lll}\left(\begin{array}{c}{x}_A^{\prime }\\ y_A^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 2\\ 0& 1\end{array}\right)\left(\begin{array}{c}{x}_A\\ y_A\end{array}\right)\\ & =& \left(\begin{array}{cc}1& 2\\ 0& 1\end{array}\right)\left(\begin{array}{c}3\\ -4\end{array}\right)\\ & =& \left(\begin{array}{c}-5\\ -4\end{array}\right)\end{array}$

Jadi, bayangan titik A(3,−4)$A(3,-4)$ oleh gusuran searah sumbu X$X$ dengan faktor skala k=2$k=2$adalah A′(−5,−4)$A^{\prime }(-5,-4)$.

Contoh 2

Tentukan bayangan garis x+2y−3=0$x+2y-3=0$ oleh gusuran searah sumbu X$X$ dengan faktor skala k=3$k=3$.

Penyelesaian:

Oleh karena matriks transformasi dari gusuran searah sumbu X$X$ dengan faktor skala k$k$adalah (10k1 )$\left(\begin{array}{cc}1& k\\ 0& 1\end{array}\right)$, maka bayangan titik (x,y)$(x,y)$ dapat ditentukan dengan cara sebagai berikut:

(x′y′ )=(1031 )(xy ) $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 3\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}$

Oleh karena AX=B⇔X=A−1B$AX=B\iff X=A^{-1}B$, maka

(xy )===11−0(10−31 )(x′y′ )(x′−3y′0+y′ )(x′−3y′y′ ) $\begin{array}{lll}\left(\begin{array}{c}x\\ y\end{array}\right)& =& \frac{1}{1-0}\left(\begin{array}{cc}1& -3\\ 0& 1\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)\\ & =& \left(\begin{array}{c}{x}^{\prime }-3y^{\prime }\\ 0+y^{\prime }\end{array}\right)\\ & =& \left(\begin{array}{c}{x}^{\prime }-3y^{\prime }\\ y^{\prime }\end{array}\right)\end{array}$

Jika kita subtitusikan hasil di atas ke dalam persamaan garis x+2y−3=0$x+2y-3=0$, maka akan kita peroleh persamaan bayangan sebagai berikut:

x+2y−3=0⇔(x′−3y′)+2y′−3=0⇔x′−y′−3=0 $\begin{array}{rl}& x+2y-3=0\\ & \iff (x^{\prime }-3y^{\prime })+2y^{\prime }-3=0\\ & \iff x^{\prime }-y^{\prime }-3=0\end{array}$

Jadi, bayangan garis x+2y−3=0$x+2y-3=0$ oleh gusuran searah sumbu X$X$ dengan faktor skala k=3$k=3$ adalah x−y−3=0$x-y-3=0$.

Nah, karena sekarang kalian sudah selesai mempelajari materi di atas, ayo kerjakan latihan soal yang ada dalam topik ini.