Gusuran Searah Sumbu Y

Gusuran Searah Sumbu Y - Pada topik sebelumnya kalian telah mengenai gusuran searah sumbu 

X$X$. Nah, dalam topik ini kalian akan belajar mengenai gusuran searah sumbu Y$Y$.

Seperti yang telah kalian ketahui, gusuran erat kaitannya dengan faktor skala. Jika arah gusuran adalah vertikal ke atas, maka faktor skala bernilai positf. Dengan kata lain, jika arah gusuran adalah vertikal ke bawah, maka faktor skala bernilai negatif.

Konsep Dasar

Tahukah kalian bentuk persamaan matriks yang sesuai dengan transformasi gusuran searah sumbu Y?

Mari kita temukan jawabannya dengan memperhatikan ilustrasi berikut:

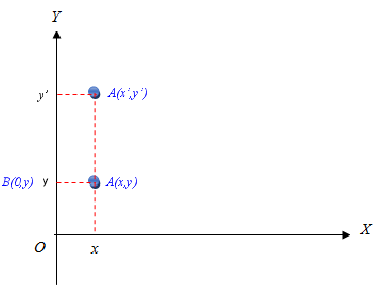
Dalam ilustrasi di atas, titik A(x,y)$A(x,y)$ digusur vertikal ke atas hingga menjadi titik A′(x′,y′)$A^{\prime }(x^{\prime },y^{\prime })$.

Nah, yang dimaksud dengan faktor skala k$k$ adalah perbandingan jarak antara AA′$A{A}^{\prime }$ dan AB$AB$. Dengan kata lain, k=AA′AB⇔k=AA′x⇔AA′=kx$k=\frac{A{A}^{\prime }}{AB}\iff k=\frac{A{A}^{\prime }}{x}\iff A{A}^{\prime }=kx$.

Dalam ilustrasi di atas, tampak bahwa

• x′=x$x^{\prime }=x$
• y′=y+AA′=y+kx$y^{\prime }=y+A{A}^{\prime }=y+kx$

Dengan demikian, persamaan matriks yang sesuai dengan transformasi gusuran searah sumbu Y$Y$ dengan faktor skala k$k$ adalah (x′y′ )=(1k01 )(xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 0\\ k& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$.

Penjelasan di atas mudah dipahami bukan?

Agar kalian semakin paham mengenai materi ini, mari kita cermati beberapa contoh berikut ini.

Contoh 1

Tentukan bayangan titik A(3,−5)$A(3,-5)$ oleh gusuran searah sumbu Y$Y$ dengan faktor skala k=2$k=2$.

Penyelesaian:

Oleh karena matriks transformasi dari gusuran searah sumbu Y$Y$ dengan faktor skala k$k$adalah (1k01 )$\left(\begin{array}{cc}1& 0\\ k& 1\end{array}\right)$, maka bayangan titik A(3,−5)$A(3,-5)$ dapat ditentukan dengan cara sebagai berikut:

(x′Ay′A )===(1201 )(xAyA )(1201 )(3−5 )(31 ) $\begin{array}{lll}\left(\begin{array}{c}{x}_A^{\prime }\\ y_A^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 0\\ 2& 1\end{array}\right)\left(\begin{array}{c}{x}_A\\ y_A\end{array}\right)\\ & =& \left(\begin{array}{cc}1& 0\\ 2& 1\end{array}\right)\left(\begin{array}{c}3\\ -5\end{array}\right)\\ & =& \left(\begin{array}{c}3\\ 1\end{array}\right)\end{array}$

Jadi, bayangan titik A(3,−5)$A(3,-5)$ oleh gusuran searah sumbu Y$Y$ dengan faktor skala k=2$k=2$adalah A′(3,1)$A^{\prime }(3,1)$.

Contoh 2

Tentukan bayangan garis x+2y−1=0$x+2y-1=0$ oleh gusuran searah sumbu Y$Y$ dengan faktor skala k=5$k=5$.

Penyelesaian:

Oleh karena matriks transformasi dari gusuran searah sumbu Y$Y$ dengan faktor skala k$k$adalah (1k01 )$\left(\begin{array}{cc}1& 0\\ k& 1\end{array}\right)$, maka bayangan titik (x,y)$(x,y)$ dapat ditentukan dengan cara sebagai berikut:

(x′y′ )=(1501 )(xy )$\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 0\\ 5& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}$

Oleh karena AX=B⇔X=A−1B$AX=B\iff X=A^{-1}B$, maka

(xy )===11−0(1−501 )(x′y′ )(x′+0−5x′+y′ )(x′−5x′+y′ ) $\begin{array}{lll}\left(\begin{array}{c}x\\ y\end{array}\right)& =& \frac{1}{1-0}\left(\begin{array}{cc}1& 0\\ -5& 1\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)\\ & =& \left(\begin{array}{c}{x}^{\prime }+0\\ -5x^{\prime }+y^{\prime }\end{array}\right)\\ & =& \left(\begin{array}{c}{x}^{\prime }\\ -5x^{\prime }+y^{\prime }\end{array}\right)\end{array}$

Jika kita subtitusikan hasil di atas ke dalam persamaan garis x+2y−1=0$x+2y-1=0$, maka akan kita peroleh persamaan bayangan sebagai berikut:

x+2y−1=0⇔x′+2(−5x′+y′)−1=0⇔x′−10x′+2y′−1=0⇔−9x′+2y′−1=0$\begin{array}{l}x+2y-1=0\\ \iff x^{\prime }+2\left(-5x^{\prime }+y^{\prime }\right)-1=0\\ \iff x^{\prime }-10x^{\prime }+2y^{\prime }-1=0\\ \iff -9x^{\prime }+2y^{\prime }-1=0\end{array}$

Jadi, bayangan garis x+2y−1=0$x+2y-1=0$ oleh gusuran searah sumbu Y$Y$ dengan faktor skala k=5$k=5$ adalah −9x+2y−1=0$-9x+2y-1=0$.

Untuk menguji pemahaman kalian mengenai materi ini, yuk kerjakan sepuluh latihan yang ada dalam topik ini.